Qué valores tienen “a” y “b” en las Cónicas?

Las cónicas son las figuras cuyo perfil aparece cuando se corta un sistema de conos unidos por los vértices.
No parece haber preferencia en el tipo de cono a utilizar, pero en entrada anterior de este blog, se propuso la conveniencia de utilizar un cono de vértice recto; con lo cual se facilita los cálculos de estudio de las figuras generadas, y el concepto de excentricidad.       

 

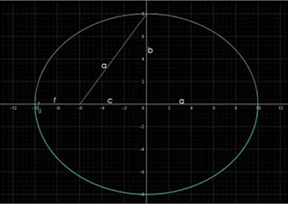
Los parámetros  a y b de las fórmulas algebraicas que representan los semiejes mayor y menor, respectivamente, de las Elipses, aparecen también en las fórmulas de las Hipérbolas, sin tener en cuenta que en esos dos tipos de figuras, esos parámetros tienen aspectos y conceptos diferentes.  (c es la distancia foco-centro).




La Elipse tiene como fórmula:


En la circunferencia, como caso especial de elipse, se encuentra que los dos parámetros a y b  son remplazados por el radio.

De hecho, teniendo en cuenta que a  y b  son habitualmente definidos como SEMIEJES mayor y menor; no existen en las Parábolas. En las Hipérbolas; abiertas y virtualmente infinitas en extensión, a  es la distancia del centro geométrico, a cada vértice.  Y dado que no existe en esas figuras un “semieje menor” desde el centro, b tendría que ser cero, indeterminado, o imaginario.   


Por facilismo a la hora de graficar, más que por  geometría, también la relación pitagórica 

             
(donde cada parámetro indica las distancias mostradas en la elipse de arriba) se ha aplicado a las Hipérbolas, aunque sea exclusiva de las elipses.   Dicha ecuación “se acomoda” en las Hipérbolas, a partir de los algoritmos que se muestran adelante.   

Como fue mencionado en entrada anterior, la excentricidad “e” puede ser asimilada a la tangente del ángulo de inclinación del corte del sistema de conos (siempre que estos sean rectos). 

O sea:                                                   

Si empleamos la ecuación

    

Puede probarse que dando a “e” valores de acuerdo a la cónica tratada  (0  para la circunferencia;  0<e<1 para las elipses; e=1 para la Parábola; y e>1 para las Hipérbolas), los valores de b cambian así:  b=a para la Circunferencia;  b=a/p(fracción de a) para las Elipses;  b=0 para la Parábola; y b=iap; para las Hipérbolas, donde i=√(-1); y p es un número positivo.  En general, si lo consideramos un par complejo; b toma valores de (a/p,0)  para las Elipses (incluyendo la circunferencia); (0,0) para la Parábola; y (0,ap) para las Hipérbolas.  Palabras más, palabras menos, los valores de b en las Hipérbolas, serían IMAGINARIOS. 

Por eso, quizás para facilitar las cosas al estudiante, no se le dice que la Fórmula para graficar las Hipérbolas no debe emplear ni a ni b; o que curiosamente la fórmula (α) aplica para las Hipérbolas (con a extraña y b imaginaria); sino que se les dice, sin más, que la fórmula para graficar las Hipérbolas es:

Puede notarse que dando a b^2 su valor negativo en las Hipérbolas, de (α) se obtiene (β), donde h y k son las coordenadas del centro de simetrías; aunque a y b son “normales” en la fórmula, pero “especiales” en la gráfica (Notemos que a se ubicaría por fuera de los cortes en los conos, si empleamos el sistema de conos cortados para representar las cónicas).

La fórmula (β) grafica perfectamente cualquier Hipérbola, pero sus parámetros a y b no son homogéneos. (a pasa de ser distancia de un punto a una curva cóncava, a distancia de un punto, a curva convexa, y b sería imaginaria).  Igual efecto tiene b en la ecuación

al tener b^2 signo negativo.  Parece otra relación, cuando en realidad es un disfraz.

Si de la ecuación de segundo grado:

hacemos B=0 y a A le asignamos signo contrario de C; con los arreglos adecuados, podemos obtener también una Hipérbola.  Esta ecuación, dadas las variables A, B, C, D, E y F, nuevas y desconocidas, puede relacionarse con (α), que contiene las variables a, b, h  y k enunciadas antes, mediante las relaciones: 

También podemos obtener una Hipérbola, si en la ecuación:

 obtenida en entrada anterior, o en su equivalente polar:

graficamos dando a e, un valor mayor que 1.

Ahora bien.  En la primera ecuación (α), ni a ni b, pueden tener valores negativos, atendiendo el hecho de que ellas representan “semiejes”, cuyos posibles valores han de ser positivos. 

En (γ); ni A ni C  pueden tener valor 0, porque no graficaría una hipérbola.

En las otras ecuaciones, donde b estaría referido en e; la relación que define dicho parámetro, es:

en virtud de que b^2 es negativo en   , al ser b imaginario.